Functional principal component analysis for longitudinal data (often abbreviated as FPCA-LD or a similar acronym) is a statistical technique used to analyze data collected over time from multiple subjects. It reduces the dimensionality of high-dimensional longitudinal data by identifying principal components that capture the most significant variation in the data across individuals and time. This allows for efficient representation of complex temporal trends, focusing on shared patterns and individual deviations. For example, analyzing growth curves for children, where height is measured repeatedly, benefits from this method to summarize growth patterns and identify subgroups with distinct growth trajectories.
The importance of this approach lies in its ability to handle the inherent correlation structure within longitudinal data. Traditional methods often struggle with such dependence. FPCA-LD effectively accounts for this correlation, providing more accurate and reliable statistical inferences. This technique facilitates efficient data visualization, allowing for easier identification of patterns and outliers. Moreover, its ability to reduce dimensionality improves model interpretability and reduces computational burden, particularly beneficial with large datasets. The development of this methodology built upon advances in functional data analysis and has significantly impacted various fields needing to analyze repeated measurements.
This discussion will now proceed to explore specific applications of this technique, examining its underlying mathematical framework, and comparing its performance against alternative methodologies for analyzing longitudinal data.
Images References

Source: www.slideserve.com
PPT Central Limit TheoremCLT PowerPoint Presentation, free download
Source: comradefinancialgroup.com
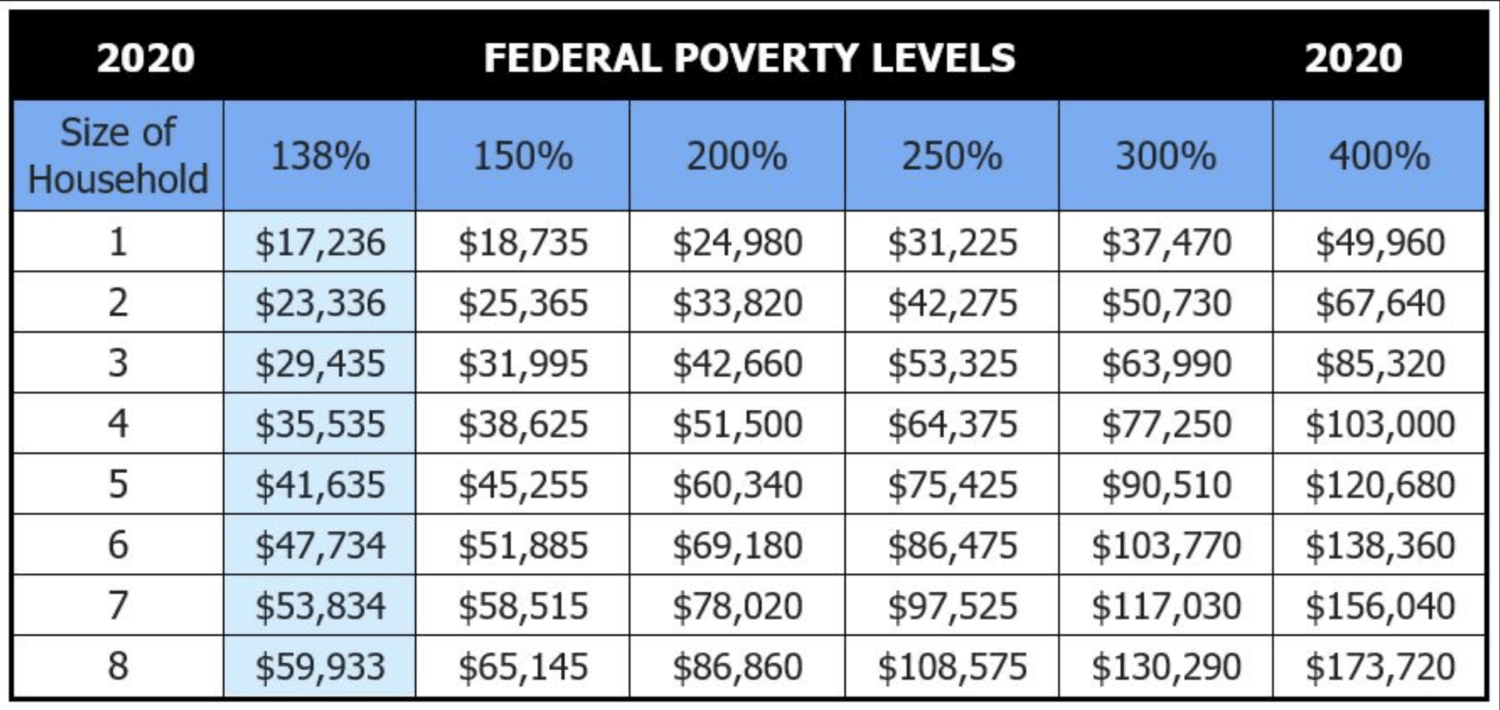
2020 Federal Poverty Level Chart Comrade Financial Group
Leave a Reply