The question of whether two numerical expressions represent the same value is fundamental to mathematics. For example, determining if the fraction 87/21 simplifies to a whole number or another fraction in its lowest terms involves simplifying the fraction by finding the greatest common divisor (GCD) of the numerator (87) and the denominator (21). In this specific case, the GCD of 87 and 21 is 3. Dividing both the numerator and the denominator by 3 yields 29/7. This indicates that 87/21 and 29/7 represent the same quantity; they are equivalent fractions.
Understanding equivalence is crucial across numerous fields. Accuracy in calculations, particularly in engineering, finance, and scientific research, hinges on precise determination of equivalence. Incorrectly assuming equivalence can lead to significant errors with potentially serious consequences. The ability to simplify fractions and identify equivalent expressions is foundational to algebraic manipulation and the development of more advanced mathematical concepts. Historical advancements in mathematics have relied on the understanding of equivalent representations to solve complex equations and prove theorems efficiently.
This understanding of numerical equivalence forms the basis for exploring topics such as rational numbers, ratio and proportion, and the simplification of complex expressions. Further examination will delve into the methods used to determine equivalence and demonstrate their application in diverse contexts.
Images References

Source: www.vecteezy.com
Age Rating sign over 21 on Transparent Background 18717860 PNG
Source: alfark6vstudyquizz.z13.web.core.windows.net
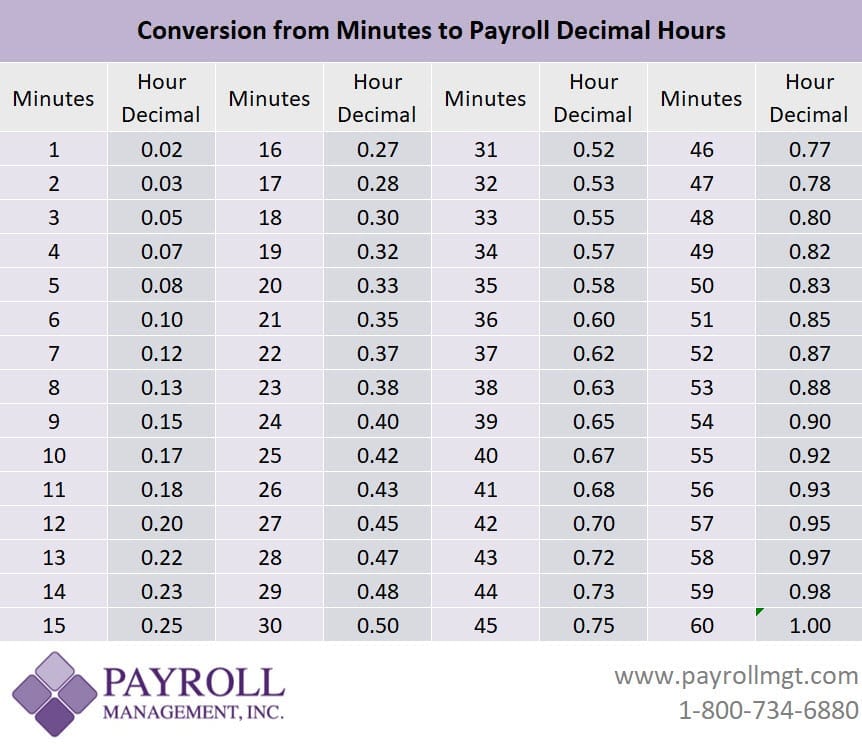
Time Conversion For Timesheet
Leave a Reply